Между населенными пунктами abcd построены дороги
Задание № 3 в ЕГЭ 2017
(в ЕГЭ 2014г - задание А2,
в ЕГЭ 2015г - задание 5)
Спецификация контрольных измерительных материалов единого государственного экзамена 2016 года по информатике и ИКТ
Практика
Т.к.теории по данному вопросу практически нет, то перейдем сразу к практике.
- Разберем примеры заданий из ЕГЭ прошлый лет.
- Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
1) 12
2) 13
3) 14
4) 16
Решать данное задание можно и устно, перебирая все возможные передвижения по сетке таблицы из исходного пункта к конечному, например:
 В данном случае, длина пути между пунктами A и F равна 2 + 3 + 9 = 14. И так далее.
В данном случае, длина пути между пунктами A и F равна 2 + 3 + 9 = 14. И так далее.
Можно еще выписывать найденные пути (АВDF = 14, и т.д.) и выбирать из них самый короткий.
Но решая таким образом, легко сделать ошибку - пропустить какой-либо путь. Поэтому я рекомендую решать такое задание полным перебором всех возможных перемещений из пункта А, составляя дерево.
Начало дерева (из пункта А можно попасть в пункты B, C, D и F):
 Первый вариант пути найден - 16.
Первый вариант пути найден - 16.
Продолжим построение.
 На этом этапе построения мы видим, что до пункта D можно добраться двумя путями и что путь через пункт В короче (2 + 3 = 5), поэтому в дальнейшем мы будем развивать именно эту ветвь дерева.
На этом этапе построения мы видим, что до пункта D можно добраться двумя путями и что путь через пункт В короче (2 + 3 = 5), поэтому в дальнейшем мы будем развивать именно эту ветвь дерева.
Продолжим построение.
 Здесь также присутствует новый путь до пункта D, но он длиннее 5, поэтому его не будем рассматривать.
Здесь также присутствует новый путь до пункта D, но он длиннее 5, поэтому его не будем рассматривать.
Продолжим построение.
 Из пункта D можно попасть в 5 пунктов, но путь в пункты A, B и С - это движение назад, поэтому остается только два пункта E и F. При этом мы нашли второй вариант пути - 2 + 3 + 9 = 14.
Из пункта D можно попасть в 5 пунктов, но путь в пункты A, B и С - это движение назад, поэтому остается только два пункта E и F. При этом мы нашли второй вариант пути - 2 + 3 + 9 = 14.
Продолжим построение.
 Находим последний вариант - 2 + 3 + 4 + 3 = 12. Он и является самым коротким.
Находим последний вариант - 2 + 3 + 4 + 3 = 12. Он и является самым коротким.
Ответ: 1.
- Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).
Это задание отличается только тем, что нет вариантов ответов, а решается точно также.
Можете себя проверить (ответ - 23).
Внимание: есть задания, в которых включено дополнительное условие, например, что нельзя проезжать через какой-либо пункт и др. Такие ветки дерева также надо отсекать.
2. Очень хорошо разобраны решения заданий ЕГЭ на сайте К.Полякова ( )
3. И, в заключение, рекомендую пройти онлайн-тест по заданию №5 (В5) на сайте К.Полякова (выбрать ) или на сайте ege.yandex.ru (
Рассмотрим решение задачи 3 ГИА 2013 по информатике
Между населёнными пунктами A, B, C, D, E, F построены дороги,
протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | F | |
| A | 3 | 5 | 15 | |||
| B | 3 | 3 | ||||
| C | 5 | 3 | 5 | 2 | ||
| D | 5 | 3 | ||||
| E | 2 | 7 | ||||
| F | 15 | 3 | 7 |
Определите длину кратчайшего пути между пунктами A и F. Передвигаться
можно только по дорогам, указанным в таблице.
1) 9 2) 11 3) 13 4) 15
Решение
Для удобства отобразим табличные данные в виде графа
Теперь переберем все возможные пути из A в F:
A-B-C-E-F = 3+3+2+7 = 15
A-B-C-D-F = 3+3+5+3 = 14
A-C-E-F = 5+2+7 = 14
A-C-D-F = 5+5+3 = 13
ну и A-F = 15
Как видно, кратчайший вариант A-C-D-F = 13км . Правильный ответ 3 .
Дополнение (ГИА 2014)
Для более качественной рассмотрим решение задачи 3 ГИА 2014 по информатике (демоверсия ФИПИ 2014)
| A | B | C | D | E | |
| A | 2 | 5 | 1 | ||
| B | 2 | 1 | |||
| C | 5 | 1 | 3 | 2 | |
| D | 1 | 3 | |||
| E | 2 |
Определите длину кратчайшего пути между пунктами A и Е. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 4 2) 5 3) 6 4) 7
Решение :
Для удобства предлагаю поступить так же, как и при решении задачи ГИА 2013 года и отобразить таблицу в виде графа. Для этого на листе расставляем точки — населенные пункты. В соответствии с таблицей соединяем их и подписываем расстояния.
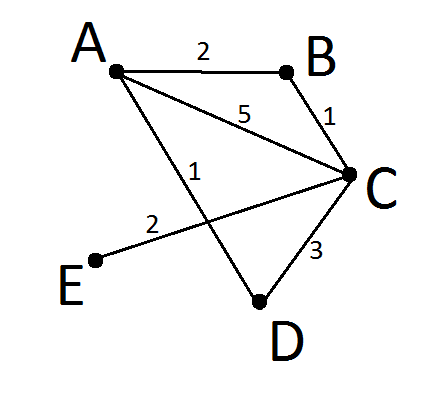
Осталось рассмотреть все возможные маршруты из A в E и найти кратчайший из них. При этом обращаем внимание на то, что в пункт E мы можем попасть только из пункта C.
A-B-C-E = 2+1+2 = 5
A-C-E = 5+2 = 7
A-D-C-E = 1+3+2 = 6
Как видим, минимальное расстояние — 5 километров (маршрут A-B-C-E). Правильный ответ 2 .
Рассмотрим решение задачи из диагностической работы ГИА по информатике 19 декабря 2013 года
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.

Определите длину кратчайшего пути между пунктами A и B (при условии, что передвигаться можно только по построенным дорогам).
1) 11 2) 12 3) 13 4) 14
Решение:
Преобразуем таблицу в граф для удобства.

Осталось перебрать все маршруты из A в B и посмотреть их длину:
A-C-D-B = 8+1+4 = 13
A-C-E-B = 8+3+1 = 12
A-D-B = 10+4 = 14
A-D-C-E-B = 10+1+3+1 = 15
Как видим, минимальный по длине маршрут A-C-E-B, который составляет 12 километров. Правильный ответ 2 .
2. Разбор демо варианта 2017
Условие задачи
На рисунке схема дорог Н-ского района изображена в виде графа; в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта Б в пункт В. В ответе запишите целое число – так, как оно указано в таблице.
Решение
Чтобы найти нужные нам вершины Б и В в весовой матрице, подсчитаем степени каждой вершины, т. е. найдем количество ребер, с которыми связана эта вершина. В матрице степень вершины - это количество непустых клето. Ниже в таблице степени вершин показаны в синем столбце (крайнем справа), а на графе показаны рядом с обозначением вершины.

По изображению на графе находим, что вершина Б имеет степень 3, а вершина В – 4. Так как в графе есть только она вершина степени 4, то вершина В - это пункт 5 (П5). Определить однозначно вершину Б мы пока не можем: в таблице это может быть П1, П2 и П4. Разберемся, какой из пунктов П1, П2 и П4 соответствует какой из вершин Б, Г и Д.
Б - единственная из этих вершин, которая соседствует с вершиной степени 2 (это вершина А). В таблице пункт степени 2 - это П6. Пункт П6 связан дорогой с П1 и не связан дорогами с П2 и П4. Поэтому вершина Б - это П1.
Теперь мы определили нужные нам вершины Б (П1) и В (П5) и можем найти ответ в весовой таблице. Смотрим на пересечение строчки П1 и столбца П5 и получаем, что искомое расстояние равно 8.
Ответ : 8.
Бонус : определим остальные вершины.
Заметим, что вершины А и Е определяются однозначно. Из вершины Е выходит одно ребро и это соответствует П3 в таблице. Вершины А имеет степень 2, и ей соответствует П6 из таблицы.
Вершина Е соединена только с одной вершиной Д. В таблице вершина Е (П3) соединена только с вершиной П4. Таким образом П4 в весовой таблице и является вершиной Д на графе.
Оставшаяся вершина П2 в весовой таблице соответствует вершине Г в графе.
3. Пример задания
2.1. Условие задачи.
Задача 2012-А2-1.
2.2. Набросок решения.
2.2.1. Перебор путей с учетом особенностей задачи
Полезно для наглядности нарисовать схему дорог (говоря «математически», - граф), соответствующий таблице. На это уйдет меньше минуты, но дальнейшее решение упростится и уменьшится риск сделать ошибку:
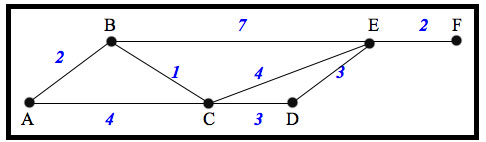
Задача поиска кратчайшего пути в графе – одна из классических задач информатики. Общий подход к ее решению приведен ниже. А пока воспользуемся тем, что граф в условии задачи – небольшой, и просто переберем все возможные пути. При этом – будем наблюдательными и постараемся сократить работу.
- В пункт F можно попасть только из пункта E. Поэтому достаточно найти кратчайший путь из A в E.
- Из A можно попасть только в B и C. Из B можно попасть в C и E. Нашелся путь ABE. Его длина – 2+7 = 9.
- Все остальные пути из A в E ведут через C.
- Из А в C есть 2 маршрута: “прямой» AC, его длина 4 и через пункт B, его длина 1+2=3. Т.е. кратчайший путь из A в C имеет длину 3.
- Из C в E есть 2 маршрута: “прямой» CE, его длина 4 и через пункт D, его длина 3+3=6. Т.е. кратчайший путь из C в E имеет длину 4.
- Таким образом, кратчайший путь из A в E, проходящий через C, - это путь ABCE, его длина 3+4=7. Это меньше, чем длина маршрута ABE. Значит, кратчайший путь из A в E имеет длину 7.
- А кратчайший маршрут из A в F – это маршрут ABCEF, его длина 7+2=9.
Ответ: 9.
2.2.2. Систематический перебор вершин
Выпишем все пути из A в F в алфавитном порядке и подсчитаем их длины. Можно рассматривать только пути без «хождения по кругу», то есть не рассматривать маршруты, которые через одну вершину проходят 2 раза. Итак.
Из A можно пойти только в B и C:
Разберемся с путями через B. Из B можно пойти в A (но это будет путь назад!), а также в C и E (это – разумные продолжения). Заменим в нашем списке путь A→B→ на два его возможных продолжения. Получим (новые верщины выделены жирным шрифтом):
A→B→ C →;
A→B→ E →;
Теперь в нашем списке – три неоконченных маршрута, они перечислены в алфавитном порядке. Снова попробуем продолжить первый из них.
Путь A→B→ C→ можно продолжить двумя способами (не считая путей назад): пойти в D или в E. Получим такой список неоконченных путей:
A→B→ C→ D →;
A→B→ C→ E →;
Путь A→B→ C→ D→ можно продолжить до пути в F только одним способом – пойти в E. Получим:
A→B→ C→ D→ E →;
A→B→ C→ E→;
Из E можно пойти только в F. Значит, из пути A→B→ C→ D→ E → мы получили полный путь A→B→ C→ D→E→F. Его длина 2+1+3+3+2 = 11.
A→B→ C→ D→E→ F . Длина 2+1+3+3+2 = 11.
A→B→ C→ E→;
Пути A→B→ C→ E→ и A→B→ E→ тоже можно завершить только одним способом. Теперь наш список путей будет выглядеть так:
A→B→ C→ D→E→ F. Длина 2+1+3+3+2 = 11.
A→B→ C→ E→F . Длина 2+1+4+2 = 9.
A→B→ E→ F . Длина 2+7+2 = 11.
Осталось разобраться с возможными продолжениями неоконченного пути A→C→. Это можно сделать точно так же, как мы поступали с продолжениями пути A→B→. У пути A→C→ есть три продолжения: A→ C→ B→E→ F, A→ C→ D→E→ F и A→C→ E→ F. Таким образом, полный список путей из A в F выглядит так:
1) A→B→ C→ D→E→ F. Длина 2+1+3+3+2 = 11.
2) A→B→ C→ E→ F. Длина 2+1+4+2 = 9.
3) A→B→ E→ F. Длина 2+7+2 = 11.
4) A→C→ B → E → F . Длина 4+1+7+2 = 14.
5) A→C→ D → E→ F . Длина 4+3+3+2 = 12.
6) A→C→ E→ F . Длина 4+4+2 = 10.
Кратчайший путь: A→B→ C→ E→ F, его длина – 9.
Ответ. Длина кратчайшего пути: 9. Правильный вариант ответа: 1.
Замечание. На практике перебор можно уменьшить. Например, если неоконченный путь длиннее, чем уже найденный полный путь, то этот неоконченный можно не продолжать. Другой пример. Сравнивая пути A→B→ C→ D→E→ F и A→B→ C→ E→ F (пути 1) и 2)), мы выяснили, что путь C→ E→ F короче, чем путь C→ D→E→ F. Поэтому при продолжении пути A→C→, вариант A→C→ D→ E→ F можно не рассматривать.
Подобные соображения можно систематизировать и получить более экономный алгоритм поиска кратчайшего пути – алгоритм Дейкстры (Эдгар Дейкстра, 1 мая 1930 г. - 6 августа 2002 – выдающийся голландский ученый, один из создателей современного программирования). Сильным ученикам его можно объяснить, однако для выполнения ЕГЭ в этом нет необходимости.
4. Еще примеры заданий.
3.1. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
|
8 |
||||||
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
3.2. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
3.3. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
3.4.
Решение. Есть прямой путь из A в Z, его длина 29. Поищем другие пути.
Видно, что сначала нужно попасть из A в C, потом - из C в F и, наконец, из F в Z. И на каждом из этих участков надо выбрать самый короткий маршрут.
Из А в С есть два маршрута – по дороге AC и через пункт B. Второй маршрут короче – его длина 3+2 = 5.
Из C в F есть много маршрутов. Однако дорога DE очень длинная и ехать по ней заведомо не стоит – получится маршрут более длинный, чем по дороге AZ. Осталось сравнить длины двух маршрутов – CDF и CEF. Более короткий маршрут – CEF, его длина 7+5 = 12 (длина маршрута CDF равна 4+11 = 15).
Наконец, из F в Z есть единственная дорога, ее длина 5. Таким образом, кратчайший маршрут из A в Z (не считая прямой дороги AZ) = это маршрут ABCEFZ. Его длина 5+ 12 + 5 = 22 < 29. Таким образом, длмна кратчайшего пути из A в Z равна 22.
Ответ: 22
3.5 Между населёнными пунктами A, B, C, D, E, F, Z построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и Z (при условии, что передвигаться можно только по построенным дорогам).
Правильные ответы : 3.1: 15; 3.2: 15; 3.3: 20; 3.4: 22; 3.5: 23
В разделе 2 приведены два решения.
Второе решение лучше тем, что оно может быть выполнено «автоматически», в отличие от первого, оно не требует от ученика никаких догадок. Если граф путей по сложности примерно такой, как в демо-версии, или даже немного сложнее, на такое решение вполне хватит двух минут. При переборе можно использовать соображения, приведенные в замечании.
В первом решении используются два дополнительных соображения. Первое соображение – выделение «узких мест», которые разбивают граф на подграфы меньшего размера; такие подграфы можно исследовать независимо или почти независимо друг от друга. В рассмотренном примере «узкие места» - это вершины D и E. Второе соображение – «длинные» ребра можно игнорировать. В примере таким ребром является ребро BE.
Таким образом, при разборе этого задания с учениками можно поступать так.
1) Научить учеников уверенно рисовать граф по заданной таблице.
2) Научить решать задачу полным перебором путей (второе решение).При этом обращать внимание на особенности задачи (как в первом решении).
3) Для сильных учеников – потренироваться в решении задачи с учетом особенностей («длинные ребра», «узловые точки» - как в первом решении).
4) *Для сильных учеников - обсудить аналогию между заданием 2 и заданием 26 (С3). Решение задания 2 с помощью составления таблиц (второе решение задачи 26 (С3)). См. лекцию М.А.Ройтберга "Графы. Подсчет путей и вариантов" в разделе





